Asymptotic behavior for a nonlocal diffusion problem with Neumann boundary conditions and a reaction term

doi:10.1285/i15900932v30n1p1

Asymptotic behavior for a nonlocal diffusion problem with Neumann boundary conditions and a reaction term

Nabongo Diabaté, Théodore K. Boni

Abstract

In this paper, we consider the following initial value problem 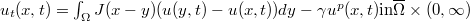$u_t(x,t)=\int_{\Omega}J(x-y)(u(y,t)-u(x,t))dy-\gamma u^{p}(x,t)& \mbox{in}& \overline{\Omega}\times(0,\infty)$ ,
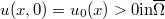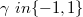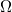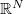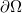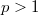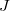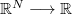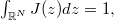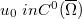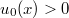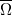$u(x,0)=u_{0}(x)>0& \mbox{in}& \overline{\Omega}$ , where $\gamma\ in \{-1,1\}$ is a parameter, $\Omega$ is a bounded domain in $\mathbb{R}^{N}$ with smooth boundary $\partial\Omega$ , $p>1$ , $J$ : $\mathbb{R}^N\longrightarrow\mathbb{R}$ is a kernel which is nonnegative, measurable, symmetric, bounded and $\int_{\mathbb{R}^N}J(z)dz=1,$ the initial datum $u_0 \ in C^0(\overline{\Omega})$ , $u_0(x)>0$ in $\overline{\Omega}$ . We show that, if 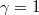$\gamma=1$ , then the solution 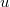$u$ of the above problem tends to zero as 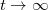$t\rightarrow\infty$ uniformly in 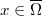$x\in\overline{\Omega}$ , and a description of its asymptotic behavior is given. We also prove that, if 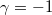$\gamma=-1$ , then the solution 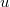$u$ blows up in a finite time, and its blow-up time goes to that of the solution of a certain ODE as the 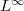$L^{\infty}$ norm of the initial datum goes to infinity.