Asymptotic behavior for a nonlocal diffusion problem with Neumann boundary conditions and a reaction term
Abstract
In this paper, we consider the following initial value problem 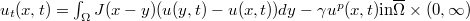 ,
,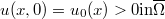 , where
, where 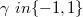 is a parameter,
is a parameter, 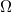 is a bounded domain in
is a bounded domain in 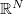 with smooth boundary
with smooth boundary 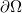 ,
, 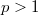 ,
, 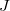 :
: 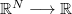 is a kernel which is nonnegative, measurable, symmetric, bounded and
is a kernel which is nonnegative, measurable, symmetric, bounded and 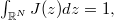 the initial datum
the initial datum 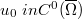 ,
, 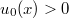 in
in 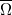 . We show that, if
. We show that, if 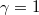 , then the solution
, then the solution 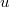 of the above problem tends to zero as
of the above problem tends to zero as 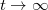 uniformly in
uniformly in 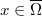 , and a description of its asymptotic behavior is given. We also prove that, if
, and a description of its asymptotic behavior is given. We also prove that, if 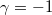 , then the solution
, then the solution 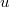 blows up in a finite time, and its blow-up time goes to that of the solution of a certain ODE as the
blows up in a finite time, and its blow-up time goes to that of the solution of a certain ODE as the 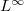 norm of the initial datum goes to infinity.
norm of the initial datum goes to infinity.
DOI Code:
10.1285/i15900932v30n1p1
Keywords:
Nonlocal diffusion; asymptotic behavior; blow-up time
Nonlocal diffusion; asymptotic behavior; blow-up time
Classification:
35B40; 45A07; 35G10
Full Text: PDF


