Email this article Using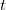 
-distribution for Robust Hierarchical Bayesian Small Area Estimation under Measurement Error in Covariates
Abstract
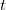-distribution with known and unknown degrees of freedom. Model parameters are estimated using a fully Bayesian framework based on MCMC methods. We validate our proposed model using simulated data and apply it to well-known crop data and the cost and income of households living in Kurdistan province of Iran.References
begin{thebibliography}{}
bibitem[Arima {em et~al.}(2015)]{Arima:Datta:Liseo:2015}
Arima, S., Datta, G.S. and Liseo, B. (2015). Bayesian estimators for small area models when auxiliary information is measured with error.
{em Scandinavian Journal of Statistics}, {bf 42}(2), 518--529.
bibitem[Akinc and Vandebroek (2018)]{Akinc:Vandebroek:2018}
Akinc, D. and Vandebroek, M. (2018). Bayesian estimation of mixed logit models: Selecting an appropriate prior for the covariance matrix.
{em Journal of choice modelling}, {bf 29}, 133--151.
bibitem[Battese {em et~al.} (1998)]{Battese:Harter:Fuller:1998}
Battese, G.E., Harter, R.M. and Fuller, W.A. (1988). An error components model for prediction of county crop areas using survey and satellite data.
{em Journal of the American Statistical Association}, {bf 83}, 28--36.
bibitem[Bell and Huang (2006)]{Bell:Huang:2006}
Bell, W.R. and Huang, E.T. (2006). Using the $t$-distribution to deal with outliers in small area estimation.
{em In Proceedings of Statistics Canada Symposium.}
bibitem[Chakraborty {em et~al.} (2017)]{Chakraborty:Datta:Mandal:2017}
Chakraborty, A., Datta, G.S. and Mandal, A. (1988). Robust hierarchical Bayes small area estimation for nested error regression model.
{em arXiv preprint arXiv:1702.05832.}
bibitem[Fay and Herriot (1979)]{Fay:Herriot:1979}
Fay, M.P. and Herriot, R.A. (1979). Estimates of income for small places: an application of
James-Stein procedures to census data.
{em Journal of the American Statistical Association}, {bf 74}(366a), 269--277.
bibitem[Ghosh {em et~al.}(2018)]{Ghosh:Myung:Moura:2018}
Ghosh, M., Myung, J. and Moura, F. A. (2018). Robust Bayesian small area estimation.
{em Survey Methodology}, {bf 44}(1), 101--116.
bibitem[Goo and Kim (2013)]{Goo:Kim:2013}
Goo, Y.M. and Kim, D.H. (2013). Bayesian small area estimations with measurement errors.
{em Journal of the Korean Data $&$ Information Science Society}, {bf 24}(4), 885--895.
bibitem[Hariyanto {em et~al.}(2020)]{Hariyanto:Notodiputro:Kurnia:Sadik:2020}
Hariyanto, S., Notodiputro, K. A., Kurnia, A. and Sadik (2020). Small Area Estimation with Measurement Error in t Distributed Covariate Variable.
{em International Journal of Advanced Science and Technology}, {bf 10}(4), 1536--1542.
bibitem[Molina and Rao (2015)]{MolinaRao:2015}
Molina, I. and J.C. Rao (2015).
newblock {em {Small Area Estimation}}.
newblock John Wiley $&$ Sons.
bibitem[Sinha and Rao (2009)]{Sinha:Rao:2009}
Sinha, S.K. and Rao, J.N.K. (2009). Robust small area estimation.
newblock {em Canadian Journal of Statistics} , {bf 37}(3), 381--399.
bibitem[Spiegelhalter {em et~al.}(2002)]{Spiegelhalter:Best:Carlin:Van:2002}
Spiegelhalter, D.J., Best, N.G., Carlin, B.P. and Van Der Linde, A. (2002). Bayesian measures of model complexity and fit.
{em Journal of the Royal Statistical Society: Series B
(Statistical Methodology)}, {bf 64}(4), 583--639.
bibitem[You and Chapman (2006)]{You:Chapman:2006}
You, Y. and Chapman, B. (2006). Small area estimation using area-level models and estimated sampling variances.
{em Survey Methodology}, {bf 1}(32), 97--103.
bibitem[Ybarra and Lohr (2008)]{Ybarra:Lohr:2008}
Ybarra, L.M. and Lohr, S.L. (2008). Small area estimation when auxiliary information is measured with error.
{em Biometrika}, {bf 95}(4), 919--931.
bibitem[Zarei {em et~al.}(2021)]{shaho:serena:Giovanna2020}
Zarei, S. and Arima, S. and Giovanna, J.L. (2021). A new robust Bayesian small area estimation via $a$-stable model for estimating the proportion of athletic students in California.
{em Biometrical Journal}, {bf 63}(6), 1309--1324
end{thebibliography}
Full Text: pdf
