Computationally efficient univariate filtering for massive data
Abstract
The vast availability of large scale, massive and big data has increased the computational cost of data analysis. One such case is the computational cost of the univariate filtering which typically involves fitting many univariate regression models and is essential for numerous variable selection algorithms to reduce the number of predictor variables. The paper manifests how to dramatically reduce that computational cost by employing the score test or the simple Pearson correlation (or the 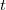 -test for binary responses). Extensive Monte Carlo simulation studies will demonstrate their advantages and disadvantages compared to the likelihood ratio test and examples with real data will illustrate the performance of the score test and the log-likelihood ratio test under realistic scenarios. Depending on the regression model used, the score test is
-test for binary responses). Extensive Monte Carlo simulation studies will demonstrate their advantages and disadvantages compared to the likelihood ratio test and examples with real data will illustrate the performance of the score test and the log-likelihood ratio test under realistic scenarios. Depending on the regression model used, the score test is 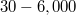 times faster than the log-likelihood ratio test and produces nearly the same results. Hence this paper strongly recommends to substitute the log-likelihood ratio test with the score test when coping with large scale data, massive data, big data, or even with data whose sample size is in the order of a few tens of thousands or higher.
times faster than the log-likelihood ratio test and produces nearly the same results. Hence this paper strongly recommends to substitute the log-likelihood ratio test with the score test when coping with large scale data, massive data, big data, or even with data whose sample size is in the order of a few tens of thousands or higher.
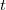 -test for binary responses). Extensive Monte Carlo simulation studies will demonstrate their advantages and disadvantages compared to the likelihood ratio test and examples with real data will illustrate the performance of the score test and the log-likelihood ratio test under realistic scenarios. Depending on the regression model used, the score test is
-test for binary responses). Extensive Monte Carlo simulation studies will demonstrate their advantages and disadvantages compared to the likelihood ratio test and examples with real data will illustrate the performance of the score test and the log-likelihood ratio test under realistic scenarios. Depending on the regression model used, the score test is 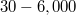 times faster than the log-likelihood ratio test and produces nearly the same results. Hence this paper strongly recommends to substitute the log-likelihood ratio test with the score test when coping with large scale data, massive data, big data, or even with data whose sample size is in the order of a few tens of thousands or higher.
times faster than the log-likelihood ratio test and produces nearly the same results. Hence this paper strongly recommends to substitute the log-likelihood ratio test with the score test when coping with large scale data, massive data, big data, or even with data whose sample size is in the order of a few tens of thousands or higher. DOI Code:
10.1285/i20705948v13n2p390
Keywords:
Univariate filtering; univariate regression models; computational efficiency
Full Text: pdf


