A Simple and Conservative Empirical Likelihood Function--Corrected

Guthrie Miller

The likelihood function

$L(\mu) = \left[1 +N\left((\mu-\overline{x})) / s \right)^2 \right]^{-n/2}$ is derived,

where 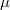$\mu$ is the true value, 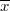$\overline{x}$ is the mean,

and 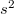$s^2$ is the variance of 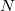$N$ measurements. This form approaches a normal for 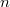$n$ large, but can be used also for 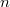$n$ small.

The use of this formula in data modeling is discussed.

DOI Code: 10.1285/i20705948v8n2p267

Keywords: likelihood function; empirical; data analysis; lognormal; probabilistic; Bayesian

%ARTICLE:

bibitem[Miller, 2014]{Miller2014}

Miller, Guthrie (2014).

newblock A Simple and Conservative Empirical Likelihood Function.

newblock {em Electronic Journal of Applied Statistical Analysis}, 7(2), pages 344--349. (2014).

%BOOK

bibitem[Miller, 2015]{Miller2015}

Miller, Guthrie (2015).

newblock {em Probabilistic Interpretation of Data--A Physicist's Approach}.

newblock Lulu Publications.

Full Text: pdf

کاغذ a4