
Il Quarderno tratta uno studio sui piani finiti di traslazione Π.
Una delle parti principali del quaderno è lo studio dei piani di traslazione di ordine n che hanno gruppi di ordine n (sezioni 11, VI, e X11). Inoltre, viene considerata la compatibilità tra elazioni e collineazioni di Baer (sezioni IV e VII) e sono presentate lezioni su piani di ordine $p^t$ che ammettono $SL(2.p^r \geq p^{t/2})$ e su piani di traslazione e parallelismi regolari.
La struttura generale di sezione 11, sezione VI e (10.3) include dei teoremi non ancora pubblicati.
Table Of Contents
| Un sillabario dei piani di traslazione |
PDF
|
|
Norman L.
Johnson
|
3-7 |
| La forma della rete derivabile in piani di traslazione di dimensione due |
PDF
|
|
Norman L.
Johnson
|
24-27 |
| Involuzioni di Baer nei piani di traslazione che hanno ampi gruppi di elazioni |
PDF
|
|
Norman L.
Johnson
|
28-36 |
| Reti derivabili che sono costruite mediante collineazioni centrali e piani di traslazione di Baer-elazione |
PDF
|
|
Norman L.
Johnson
|
37-52 |
| Piani di traslazione di ordine n con gruppi abeliani di collineazioni di ordine n |
PDF
|
|
Norman L.
Johnson
|
92-95 |
| La questione della linearità per i gruppi abeliani nei piani di traslazione |
PDF
|
|
Norman L.
Johnson
|
96-101 |
| Parallelismi regolari e piani di traslazione |
PDF
|
|
Norman L.
Johnson
|
108-115 |
| Bibliografia |
PDF
|
|
Norman L.
Johnson
|
116-121 |
Questo sito utilizza un cookie tecnico per consentire la corretta navigazione. Se vuoi saperne di più consulta l'
informativa estesa.
 This work is licensed under a Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0 Italia License.
This work is licensed under a Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0 Italia License.

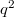 che hanno un gruppo di collineazioni di ordine
che hanno un gruppo di collineazioni di ordine 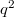 ; l'orbita regolare
; l'orbita regolare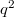 che hanno un gruppo di collineazioni di ordine
che hanno un gruppo di collineazioni di ordine 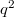 che non agisce regolarmente
che non agisce regolarmente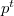 che hanno un gruppo di collineazioni isomorfo a
che hanno un gruppo di collineazioni isomorfo a 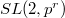 con r maggiore di
con r maggiore di 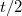
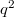 ,q pari,che hanno 2-sottogruppi di Baer di ordine maggiore di
,q pari,che hanno 2-sottogruppi di Baer di ordine maggiore di 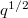
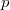 che ammettono gruppi non solubili i cui p-sottogruppi di Silow sono gruppi planari
che ammettono gruppi non solubili i cui p-sottogruppi di Silow sono gruppi planari

