Introduzione
Abstract
En
An axiomatic approach to classical kinematics is developed. An affine four dimensional space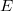 (event space), a three dimensional subspace(Error rendering LaTeX formula) (simultaneity space), an euclidean conformal metric G on(Error rendering LaTeX formula) and an orientation on
(event space), a three dimensional subspace(Error rendering LaTeX formula) (simultaneity space), an euclidean conformal metric G on(Error rendering LaTeX formula) and an orientation on 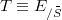 (time) constitute the general framework. The one-body absolute kinematics considers an absolute motion(Error rendering LaTeX formula), its absolute velocity
(time) constitute the general framework. The one-body absolute kinematics considers an absolute motion(Error rendering LaTeX formula), its absolute velocity 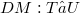 and accelaration
and accelaration 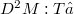 . The continum absolute kinematics considers a family of disjoint motions filling E and their velocities, accelerations and jacobians. A continum can be taken as a frame of reference, for it determines the position map
. The continum absolute kinematics considers a family of disjoint motions filling E and their velocities, accelerations and jacobians. A continum can be taken as a frame of reference, for it determines the position map 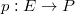 . The set of position P is a C∈fty manifold, diffeomorphic to affine three dimensional spaces and endowed with a time depending metric
. The set of position P is a C∈fty manifold, diffeomorphic to affine three dimensional spaces and endowed with a time depending metric 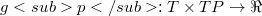 , a time depending affine connection
, a time depending affine connection 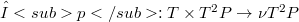 , a Coriolis map
, a Coriolis map 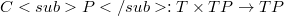 and a dragging map
and a dragging map 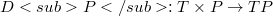 . A classification of special frames considers affine, rigid, translating and inertial frames, characterized by the properties of their motions and their position spaces. The observed kinematics condiders the observed motion
. A classification of special frames considers affine, rigid, translating and inertial frames, characterized by the properties of their motions and their position spaces. The observed kinematics condiders the observed motion 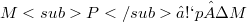 , its velocity and acceleration and compares them with the absolute quantities. By comparison of observed kinematics, with respect to two frames, the addition velocities and generalized Coriolis theorem is obtained.
, its velocity and acceleration and compares them with the absolute quantities. By comparison of observed kinematics, with respect to two frames, the addition velocities and generalized Coriolis theorem is obtained.
An axiomatic approach to classical kinematics is developed. An affine four dimensional space
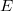 (event space), a three dimensional subspace(Error rendering LaTeX formula) (simultaneity space), an euclidean conformal metric G on(Error rendering LaTeX formula) and an orientation on
(event space), a three dimensional subspace(Error rendering LaTeX formula) (simultaneity space), an euclidean conformal metric G on(Error rendering LaTeX formula) and an orientation on 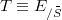 (time) constitute the general framework. The one-body absolute kinematics considers an absolute motion(Error rendering LaTeX formula), its absolute velocity
(time) constitute the general framework. The one-body absolute kinematics considers an absolute motion(Error rendering LaTeX formula), its absolute velocity 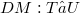 and accelaration
and accelaration 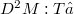 . The continum absolute kinematics considers a family of disjoint motions filling E and their velocities, accelerations and jacobians. A continum can be taken as a frame of reference, for it determines the position map
. The continum absolute kinematics considers a family of disjoint motions filling E and their velocities, accelerations and jacobians. A continum can be taken as a frame of reference, for it determines the position map 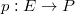 . The set of position P is a C∈fty manifold, diffeomorphic to affine three dimensional spaces and endowed with a time depending metric
. The set of position P is a C∈fty manifold, diffeomorphic to affine three dimensional spaces and endowed with a time depending metric 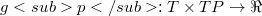 , a time depending affine connection
, a time depending affine connection 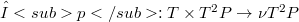 , a Coriolis map
, a Coriolis map 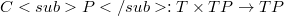 and a dragging map
and a dragging map 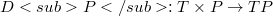 . A classification of special frames considers affine, rigid, translating and inertial frames, characterized by the properties of their motions and their position spaces. The observed kinematics condiders the observed motion
. A classification of special frames considers affine, rigid, translating and inertial frames, characterized by the properties of their motions and their position spaces. The observed kinematics condiders the observed motion 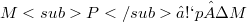 , its velocity and acceleration and compares them with the absolute quantities. By comparison of observed kinematics, with respect to two frames, the addition velocities and generalized Coriolis theorem is obtained.
, its velocity and acceleration and compares them with the absolute quantities. By comparison of observed kinematics, with respect to two frames, the addition velocities and generalized Coriolis theorem is obtained.DOI Code:
§
Full Text: PDF


