Fullness and scalar curvature of the totally real submanifolds in 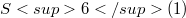
Abstract
Let M be a totally rea1 3-dimensional submanifold of the nearly Kähler 6-sphere 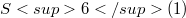 . Theorems are proven on the relation between the fullness and the scalar curvature R of M. In particular, if either R is a constant different from 2, or M is compact with
. Theorems are proven on the relation between the fullness and the scalar curvature R of M. In particular, if either R is a constant different from 2, or M is compact with 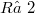 , then M is full in
, then M is full in 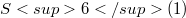 unless M is totally geodesic. A family of examples with
unless M is totally geodesic. A family of examples with 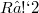 , which are fully contained in some great hypersphere
, which are fully contained in some great hypersphere 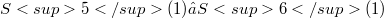 , are also defined in an explicit manner.
, are also defined in an explicit manner.
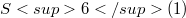 . Theorems are proven on the relation between the fullness and the scalar curvature R of M. In particular, if either R is a constant different from 2, or M is compact with
. Theorems are proven on the relation between the fullness and the scalar curvature R of M. In particular, if either R is a constant different from 2, or M is compact with 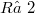 , then M is full in
, then M is full in 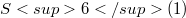 unless M is totally geodesic. A family of examples with
unless M is totally geodesic. A family of examples with 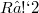 , which are fully contained in some great hypersphere
, which are fully contained in some great hypersphere 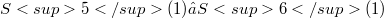 , are also defined in an explicit manner.
, are also defined in an explicit manner.DOI Code:
10.1285/i15900932v16n1p105
Keywords:
Fullness scalar curvature; Totally real submanifolds; Nearly Kähler structure; Minimality
Classification:
53C42
Full Text: PDF


