Coefficient multipliers with closed range
Abstract
For two power series 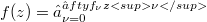 and
and 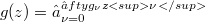 with positive radii of convergence, the Hadamard product or convolution is defined by
with positive radii of convergence, the Hadamard product or convolution is defined by 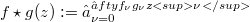 . We consider the prblem of characterizing those convolution operators
. We consider the prblem of characterizing those convolution operators 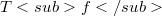 acting on spaces of holomorphic functions which have closed range. In particular, we show that every Euler differential operator
acting on spaces of holomorphic functions which have closed range. In particular, we show that every Euler differential operator 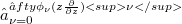 is a convolution operator
is a convolution operator 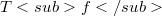 and we characterize the Euler differential operators, which are surjective on the space of holomorphic functions on every domain which contains the origin.
and we characterize the Euler differential operators, which are surjective on the space of holomorphic functions on every domain which contains the origin.
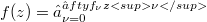 and
and 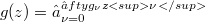 with positive radii of convergence, the Hadamard product or convolution is defined by
with positive radii of convergence, the Hadamard product or convolution is defined by 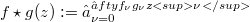 . We consider the prblem of characterizing those convolution operators
. We consider the prblem of characterizing those convolution operators 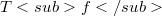 acting on spaces of holomorphic functions which have closed range. In particular, we show that every Euler differential operator
acting on spaces of holomorphic functions which have closed range. In particular, we show that every Euler differential operator 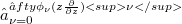 is a convolution operator
is a convolution operator 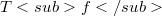 and we characterize the Euler differential operators, which are surjective on the space of holomorphic functions on every domain which contains the origin.
and we characterize the Euler differential operators, which are surjective on the space of holomorphic functions on every domain which contains the origin.DOI Code:
10.1285/i15900932v17p61
Full Text: PDF


