A representation formula for weakly compact starshaped sets
Abstract
Let S be a nonconvex weakly compact and weakly connected subset of a real locally convex topological linear space L and D a relatively weakly open subset of S containing the set Inc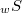 of local nonconvexity points of S with respect to the weak topology. It is proved that ker
of local nonconvexity points of S with respect to the weak topology. It is proved that ker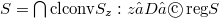 , where regS denotes the set of regular points of S and
, where regS denotes the set of regular points of S and 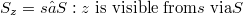 . This substantially stregthens a recent result of Stavrakas in which the intersection above was taken over the whole set regS. The intersection formula is shown to hold also for a nonconvex connected weakly compact subset S of L with D being a relatively weakly open subset of S containing the set IncS of local nonconvexity points of S.
. This substantially stregthens a recent result of Stavrakas in which the intersection above was taken over the whole set regS. The intersection formula is shown to hold also for a nonconvex connected weakly compact subset S of L with D being a relatively weakly open subset of S containing the set IncS of local nonconvexity points of S.
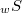 of local nonconvexity points of S with respect to the weak topology. It is proved that ker
of local nonconvexity points of S with respect to the weak topology. It is proved that ker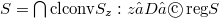 , where regS denotes the set of regular points of S and
, where regS denotes the set of regular points of S and 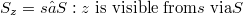 . This substantially stregthens a recent result of Stavrakas in which the intersection above was taken over the whole set regS. The intersection formula is shown to hold also for a nonconvex connected weakly compact subset S of L with D being a relatively weakly open subset of S containing the set IncS of local nonconvexity points of S.
. This substantially stregthens a recent result of Stavrakas in which the intersection above was taken over the whole set regS. The intersection formula is shown to hold also for a nonconvex connected weakly compact subset S of L with D being a relatively weakly open subset of S containing the set IncS of local nonconvexity points of S.DOI Code:
10.1285/i15900932v19n2p207
Full Text: PDF


