A viscoelastic fluid flow through mixing grids
Abstract
We study the asymtotic behaviour of a viscoelastic fluid in a porous medium 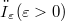 obtained by removing from an open set
obtained by removing from an open set  small obstacles
small obstacles 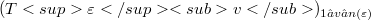 of size
of size 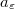 periodically distributed on a hyperplane H which intersects
periodically distributed on a hyperplane H which intersects  . We establish that the fluid behave differently depending on whether the size
. We establish that the fluid behave differently depending on whether the size 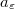 is greater than or smaller than a critical size
is greater than or smaller than a critical size 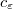 . If
. If 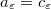 , a convolution term appears in the limit problem. This corresponds to a long memory effect. If
, a convolution term appears in the limit problem. This corresponds to a long memory effect. If 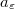 is smaller than
is smaller than 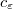 , the fluid behaves as if there where no obstacles. If
, the fluid behaves as if there where no obstacles. If 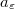 is greater than
is greater than 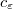 or is of the order of the period, the fluid adheres on the hyperplane H which plays a thin solid plate role and the fluid behaves separately on each side of this plate.
or is of the order of the period, the fluid adheres on the hyperplane H which plays a thin solid plate role and the fluid behaves separately on each side of this plate.
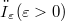 obtained by removing from an open set
obtained by removing from an open set  small obstacles
small obstacles 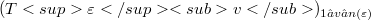 of size
of size 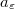 periodically distributed on a hyperplane H which intersects
periodically distributed on a hyperplane H which intersects  . We establish that the fluid behave differently depending on whether the size
. We establish that the fluid behave differently depending on whether the size 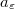 is greater than or smaller than a critical size
is greater than or smaller than a critical size 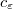 . If
. If 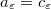 , a convolution term appears in the limit problem. This corresponds to a long memory effect. If
, a convolution term appears in the limit problem. This corresponds to a long memory effect. If 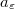 is smaller than
is smaller than 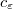 , the fluid behaves as if there where no obstacles. If
, the fluid behaves as if there where no obstacles. If 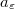 is greater than
is greater than 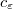 or is of the order of the period, the fluid adheres on the hyperplane H which plays a thin solid plate role and the fluid behaves separately on each side of this plate.
or is of the order of the period, the fluid adheres on the hyperplane H which plays a thin solid plate role and the fluid behaves separately on each side of this plate.DOI Code:
10.1285/i15900932v19n2p153
Full Text: PDF


