The natural affinors on 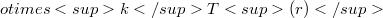
Abstract
For integers 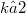 , r and
, r and 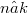 we prove that any natural affinor A on the k-tensor power
we prove that any natural affinor A on the k-tensor power 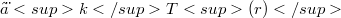 of the linear r-tangent bundle functor T(r) over n-manifolds is proportional to the identity affinor.
of the linear r-tangent bundle functor T(r) over n-manifolds is proportional to the identity affinor.
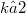 , r and
, r and 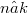 we prove that any natural affinor A on the k-tensor power
we prove that any natural affinor A on the k-tensor power 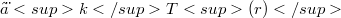 of the linear r-tangent bundle functor T(r) over n-manifolds is proportional to the identity affinor.
of the linear r-tangent bundle functor T(r) over n-manifolds is proportional to the identity affinor.DOI Code:
10.1285/i15900932v19n2p269
Keywords:
Bundle hunters; Natural transformations; Natural affinors
Classification:
58A20; 53A55
Full Text: PDF


