Note on squarefree integers through a set theoretical property
Abstract
In this paper, we show a property of set theory, that in number theory has the following consequence: if 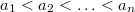 are squarefree integers, then the number of distinct ratios
are squarefree integers, then the number of distinct ratios 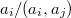 is greater than or equal to n, where
is greater than or equal to n, where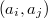 denotes the greatest common divisor of
denotes the greatest common divisor of 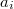 and
and 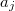 .
.
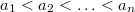 are squarefree integers, then the number of distinct ratios
are squarefree integers, then the number of distinct ratios 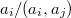 is greater than or equal to n, where
is greater than or equal to n, where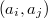 denotes the greatest common divisor of
denotes the greatest common divisor of 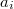 and
and 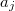 .
.DOI Code:
10.1285/i15900932v19n2p227
Full Text: PDF


