Geodesic generators of 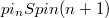
Abstract
We show for all 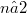 the cartan inclusion of
the cartan inclusion of 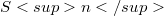 in
in 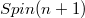 , as a totally geodesic submanifold of constant sectional curvature, generates a cyclic direct summand of
, as a totally geodesic submanifold of constant sectional curvature, generates a cyclic direct summand of 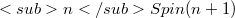 .
.
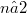 the cartan inclusion of
the cartan inclusion of 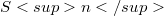 in
in 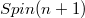 , as a totally geodesic submanifold of constant sectional curvature, generates a cyclic direct summand of
, as a totally geodesic submanifold of constant sectional curvature, generates a cyclic direct summand of 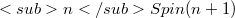 .
.DOI Code:
10.1285/i15900932v19n2p219
Full Text: PDF


