Homogeneous Manifolds in Codimension Two Revisited
Abstract
In this paper we study Riemannian homogeneous submanifolds of Euclidean spaces in codimension two. If the index of relative nullity of the second fundamental form is relatively low, we prove that the submanifold is a product 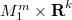 where
where 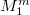 is either isometric to a sphere or to a compact isoparametric hypersurface of the sphere or covered by
is either isometric to a sphere or to a compact isoparametric hypersurface of the sphere or covered by 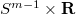 . For homogeneous Einstein manifolds we obtain a complete classification which improves the result in [1].
. For homogeneous Einstein manifolds we obtain a complete classification which improves the result in [1].
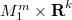 where
where 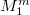 is either isometric to a sphere or to a compact isoparametric hypersurface of the sphere or covered by
is either isometric to a sphere or to a compact isoparametric hypersurface of the sphere or covered by 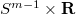 . For homogeneous Einstein manifolds we obtain a complete classification which improves the result in [1].
. For homogeneous Einstein manifolds we obtain a complete classification which improves the result in [1].DOI Code:
10.1285/i15900932v21n1p49
Keywords:
Relative nullity; Rigid immersions; Isometry; Einstein manifolds
Classification:
53C40; 53C42
Full Text: PDF


