An Eightfold Littlewood-Richardson Theorem

Abstract

Based on a generalized ordering 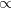on a set 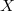, Schensted's  insertion mapping is defined on the set of words 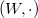over the ordered alphabet 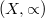. In this general framework, a transparent approach to various versions of the Robinson-Schensted correspondence and of invariant properties originally due to Schützenberger, Knuth, White e.a. is obtained.  Furthermore, eight combinatorial descriptions of the Littlewood-Richardson coefficients are obtained simultaneously, and direct bijections between the corresponding sets, including the bijection of Hanlon and Sundaram. Some of these descriptions may be translated into identities of skew Schur functions discovered by Aitken and Berenstein/Zelevinsky.