Upper semicontinuity of the spectrum function and automatic continuity in topological 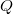 -algebras
-algebras
Abstract
In 1993, M. Fragoulopoulou applied thetechnique of Ransford and proved that if 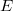 and
and 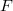 are lmcalgebras such that
are lmcalgebras such that 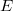 is a Q-algebra,
is a Q-algebra, 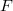 is semisimple andadvertibly complete, and
is semisimple andadvertibly complete, and 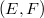 is a closed graph pair, then eachsurjective homomorphism
is a closed graph pair, then eachsurjective homomorphism 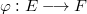 is continuous. Later onin 1996, it was shown by Akkar and Nacir that if
is continuous. Later onin 1996, it was shown by Akkar and Nacir that if 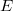 and
and 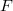 areboth LFQ-algebras and
areboth LFQ-algebras and 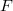 is semisimple then evey surjectivehomomorphism
is semisimple then evey surjectivehomomorphism 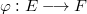 is continuous. In this work weextend the above results by removing the lmc property from
is continuous. In this work weextend the above results by removing the lmc property from 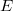 .
.
We first show that in a topological algebra, the uppersemicontinuity of the spectrum function, the upper semicontinuityof the spectral radius function, the continuity of the spectralradius function at zero, and being a 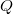 -algebra, are allequivalent. Then it is shown that if
-algebra, are allequivalent. Then it is shown that if 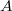 is a topological
is a topological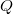 -algebra and
-algebra and 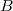 is an lmc semisimple algebra which isadvertibly complete, then every surjective homomorphism
is an lmc semisimple algebra which isadvertibly complete, then every surjective homomorphism 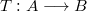 has a closed graph. In particular, if
has a closed graph. In particular, if 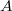 is a Q-algebra with acomplete metrizable topology, and
is a Q-algebra with acomplete metrizable topology, and 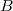 is a semisimple Fréchet algebra, then every surjective homomorphism
is a semisimple Fréchet algebra, then every surjective homomorphism 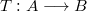 isautomatically continuous.
isautomatically continuous.
Full Text: PDF


