An Analysis of Quasilinear Elliptic Systems with 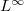 -Type Data
-Type Data
Abstract
The present study establishes the existence and uniqueness of a solution of weak energy for a boundary value problem within a smooth, bounded, open domain 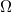 in
in 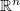 where
where 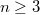 . The problem is defined by the following equation:
. The problem is defined by the following equation: ![\begin{cases} {-div} \left[a(z,\upsilon,D\upsilon)\right]+\vert \upsilon\vert^{p{(z)}-2}\upsilon =f & \text { in } \Omega, \\ ~~ \upsilon =0 & \text { on } \partial \Omega, \end{cases}](http://siba-ese.unile.it/plugins/generic/latexRender/cache/914c59fbbf77be2dc02681892219ded1.png) where the function
where the function 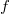 is constrained to lie within the space
is constrained to lie within the space 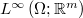 . The proof of existence relies on the utilization of the concept of Young measures.
. The proof of existence relies on the utilization of the concept of Young measures.
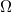 in
in 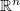 where
where 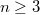 . The problem is defined by the following equation:
. The problem is defined by the following equation: ![\begin{cases} {-div} \left[a(z,\upsilon,D\upsilon)\right]+\vert \upsilon\vert^{p{(z)}-2}\upsilon =f & \text { in } \Omega, \\ ~~ \upsilon =0 & \text { on } \partial \Omega, \end{cases}](http://siba-ese.unile.it/plugins/generic/latexRender/cache/914c59fbbf77be2dc02681892219ded1.png) where the function
where the function 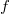 is constrained to lie within the space
is constrained to lie within the space 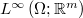 . The proof of existence relies on the utilization of the concept of Young measures.
. The proof of existence relies on the utilization of the concept of Young measures.DOI Code:
10.1285/i15900932v44n2p113
Keywords:
Quasilinear elliptic systems; weak energy solution; Young measure; p(z)-variable exponents
Full Text: PDF


