On ideal and subalgebra coefficients in a class k-algebras
Abstract
Let k be a commutative field with prime field 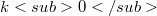 and A a k- algebra. Moreover, assume that there is a k-vector space basis
and A a k- algebra. Moreover, assume that there is a k-vector space basis  of A that satisfies the following condition: for all
of A that satisfies the following condition: for all 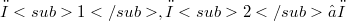 ,the product
,the product 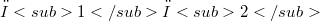 is contained in the
is contained in the 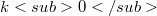 -vector space spanned by
-vector space spanned by  . It is proven that the concept of minimal field of definition from polynomial rings and semigroup algebras can be generalized to the above class of (not necessarily associative) k-algebras. Namely, let U be a one-sided ideal in A or a k-subalgebra of A. Then there exists a smallest
. It is proven that the concept of minimal field of definition from polynomial rings and semigroup algebras can be generalized to the above class of (not necessarily associative) k-algebras. Namely, let U be a one-sided ideal in A or a k-subalgebra of A. Then there exists a smallest 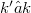 with U-as one-sided ideal resp. as k-algebra—being generated by elements in the
with U-as one-sided ideal resp. as k-algebra—being generated by elements in the 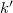 -vector space spanned by
-vector space spanned by  .
.
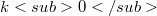 and A a k- algebra. Moreover, assume that there is a k-vector space basis
and A a k- algebra. Moreover, assume that there is a k-vector space basis  of A that satisfies the following condition: for all
of A that satisfies the following condition: for all 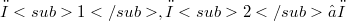 ,the product
,the product 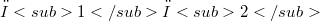 is contained in the
is contained in the 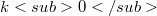 -vector space spanned by
-vector space spanned by  . It is proven that the concept of minimal field of definition from polynomial rings and semigroup algebras can be generalized to the above class of (not necessarily associative) k-algebras. Namely, let U be a one-sided ideal in A or a k-subalgebra of A. Then there exists a smallest
. It is proven that the concept of minimal field of definition from polynomial rings and semigroup algebras can be generalized to the above class of (not necessarily associative) k-algebras. Namely, let U be a one-sided ideal in A or a k-subalgebra of A. Then there exists a smallest 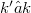 with U-as one-sided ideal resp. as k-algebra—being generated by elements in the
with U-as one-sided ideal resp. as k-algebra—being generated by elements in the 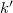 -vector space spanned by
-vector space spanned by  .
.DOI Code:
10.1285/i15900932v27n1p77
Keywords:
Field of definition; Non-associative k-algebra; One-sided ideal; k-subalgebra
Full Text: PDF PS


