Some results on almost Kenmotsu manifolds
Abstract
First we consider almost Kenmotsu manifolds which satisfy Codazzi condition for 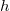 and
and 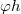 , and we prove that in such cases the tensor
, and we prove that in such cases the tensor 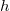 vanishes. Next, we prove that an almost Kenmotsu manifold having constant
vanishes. Next, we prove that an almost Kenmotsu manifold having constant 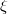 -sectional curvature
-sectional curvature 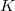 which is locally symmetric is a Kenmotsu manifold of constant curvature
which is locally symmetric is a Kenmotsu manifold of constant curvature 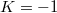 . We also prove that, for a
. We also prove that, for a 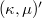 -almost Kenmotsu manifold of
-almost Kenmotsu manifold of 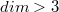 with
with 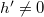 , every conformal vector field is Killing. Finally, we prove that if
, every conformal vector field is Killing. Finally, we prove that if 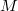 is a
is a 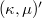 -almost Kenmotsu manifold with
-almost Kenmotsu manifold with 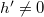 and
and 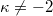 , then the vector field
, then the vector field 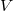 which leaves the curvature tensor invariant is Killing.
which leaves the curvature tensor invariant is Killing.
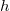 and
and 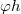 , and we prove that in such cases the tensor
, and we prove that in such cases the tensor 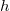 vanishes. Next, we prove that an almost Kenmotsu manifold having constant
vanishes. Next, we prove that an almost Kenmotsu manifold having constant 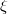 -sectional curvature
-sectional curvature 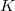 which is locally symmetric is a Kenmotsu manifold of constant curvature
which is locally symmetric is a Kenmotsu manifold of constant curvature 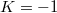 . We also prove that, for a
. We also prove that, for a 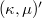 -almost Kenmotsu manifold of
-almost Kenmotsu manifold of 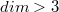 with
with 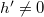 , every conformal vector field is Killing. Finally, we prove that if
, every conformal vector field is Killing. Finally, we prove that if 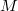 is a
is a 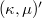 -almost Kenmotsu manifold with
-almost Kenmotsu manifold with 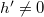 and
and 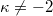 , then the vector field
, then the vector field 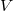 which leaves the curvature tensor invariant is Killing.
which leaves the curvature tensor invariant is Killing.DOI Code:
10.1285/i15900932v40n1p87
Keywords:
Almost Kenmotsu manifold; Locally symmetric spaces; Infinitesimal contact transformation; Conformal vector field
Full Text: PDF


