Cones in 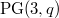
Abstract
In this paper, sets of points of 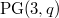 of size
of size 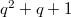 and intersecting every plane in
and intersecting every plane in 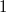 ,
, 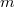 or
or 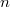 points are studied.
points are studied.
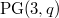 of size
of size 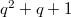 and intersecting every plane in
and intersecting every plane in 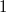 ,
, 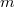 or
or 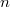 points are studied.
points are studied.DOI Code:
10.1285/i15900932v40n1p81
Keywords:
projective space; ovals; quadratic cones; intersection number
Full Text: PDF


