On rings and Banach algebras with skew derivations
Abstract
In the present paper, we investigate the commutativity of a prime Banach algebra with skew derivations and prove that if  is prime Banach algebra and
is prime Banach algebra and  has a nonzero continuous linear skew derivation
has a nonzero continuous linear skew derivation  from
from  to
to  such that
such that ![[\f(\xa^{m}), \f(\ya^{n})] - [\xa^{m}, \ya^{n}] \in \z(\Aa)](http://siba-ese.unile.it/plugins/generic/latexRender/cache/6d17e8ccaf6aa5dad4363c503f44b1ac.png) for an integers
for an integers 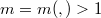 and
and 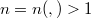 and sufficiently many
and sufficiently many  , then
, then  is commutative.
is commutative.
 is prime Banach algebra and
is prime Banach algebra and  has a nonzero continuous linear skew derivation
has a nonzero continuous linear skew derivation  from
from  to
to  such that
such that ![[\f(\xa^{m}), \f(\ya^{n})] - [\xa^{m}, \ya^{n}] \in \z(\Aa)](http://siba-ese.unile.it/plugins/generic/latexRender/cache/6d17e8ccaf6aa5dad4363c503f44b1ac.png) for an integers
for an integers 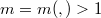 and
and 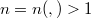 and sufficiently many
and sufficiently many  , then
, then  is commutative.
is commutative.DOI Code:
10.1285/i15900932v40n1p73
Keywords:
Prime Banach algebra; skew derivation
Full Text: PDF


