Generalization of certain well-known inequalities for rational functions
Abstract
Let 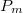 be a class of all polynomials of degree at most m and let
be a class of all polynomials of degree at most m and let 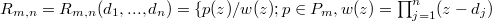 where
where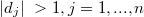 and
and 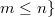 denote the class of rational functions. It is proved that if the rational function
denote the class of rational functions. It is proved that if the rational function 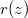 having all its zeros in
having all its zeros in 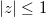 , then for
, then for 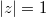
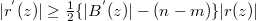 .
.
The main purpose of this paper is to improve the above inequality for rational functions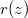 having all its zeros in
having all its zeros in 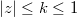 with
with 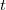 -fold zeros at the origin and some other related inequalities. The obtained results sharpen some well-known estimates for the derivative and polar derivative of polynomials.
-fold zeros at the origin and some other related inequalities. The obtained results sharpen some well-known estimates for the derivative and polar derivative of polynomials.
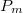 be a class of all polynomials of degree at most m and let
be a class of all polynomials of degree at most m and let 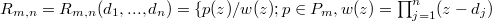 where
where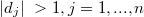 and
and 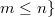 denote the class of rational functions. It is proved that if the rational function
denote the class of rational functions. It is proved that if the rational function 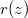 having all its zeros in
having all its zeros in 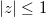 , then for
, then for 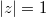
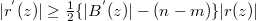 .
. The main purpose of this paper is to improve the above inequality for rational functions
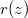 having all its zeros in
having all its zeros in 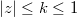 with
with 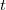 -fold zeros at the origin and some other related inequalities. The obtained results sharpen some well-known estimates for the derivative and polar derivative of polynomials.
-fold zeros at the origin and some other related inequalities. The obtained results sharpen some well-known estimates for the derivative and polar derivative of polynomials.DOI Code:
10.1285/i15900932v40n1p1
Keywords:
Rational functions; Polynomials; Polar derivative; Inequalities; Poles; Restricted Zeros
Full Text: PDF


