Existence and multiplicity results for a doubly anisotropic problem with sign-changing nonlinearity
Abstract
We consider in this paper the following problem
![-\sum\limits_{i=1}^{N}\partial _{i}\left[ \left\vert \partial _{i}u\right\vert ^{p_{i}-2}\partial _{i}u\right] -\sum\limits_{i=1}^{N} \partial _{i}\left[ \left\vert \partial _{i}u\right\vert ^{q_{i}-2}\partial _{i}u\right] =\lambda f(u) \text{ \ }\ \text{in } \Omega,\\](http://siba-ese.unile.it/plugins/generic/latexRender/cache/20e2262caa4b1f4c64af3b33c86c6b57.png)

Where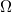 is a bounded regular domain in
is a bounded regular domain in 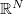 ,
,  and
and 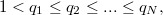 we will also assume that
we will also assume that 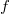 is a continuous function, that have a finite number of zeroes, changing sign between them.
is a continuous function, that have a finite number of zeroes, changing sign between them.
![-\sum\limits_{i=1}^{N}\partial _{i}\left[ \left\vert \partial _{i}u\right\vert ^{p_{i}-2}\partial _{i}u\right] -\sum\limits_{i=1}^{N} \partial _{i}\left[ \left\vert \partial _{i}u\right\vert ^{q_{i}-2}\partial _{i}u\right] =\lambda f(u) \text{ \ }\ \text{in } \Omega,\\](http://siba-ese.unile.it/plugins/generic/latexRender/cache/20e2262caa4b1f4c64af3b33c86c6b57.png)

Where
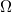 is a bounded regular domain in
is a bounded regular domain in 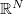 ,
,  and
and 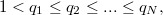 we will also assume that
we will also assume that 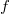 is a continuous function, that have a finite number of zeroes, changing sign between them.
is a continuous function, that have a finite number of zeroes, changing sign between them.DOI Code:
10.1285/i15900932v39n2p1
Keywords:
Anisotropic problem; exitence and mutiplicity; variational methods
Full Text: PDF


