Non-existence of smooth rational curves of degree d = 13, 14, 15 con-tained in a general quintic hypersurface of P4 and in some quadric hypersurface
Abstract
Let 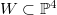 be a general quintic hypersurface. We prove that
be a general quintic hypersurface. We prove that 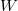 contains no smooth rational curve
contains no smooth rational curve 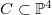 with degree
with degree 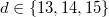 ,
, 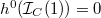 and
and 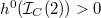 .
.
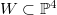 be a general quintic hypersurface. We prove that
be a general quintic hypersurface. We prove that 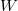 contains no smooth rational curve
contains no smooth rational curve 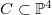 with degree
with degree 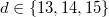 ,
, 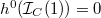 and
and 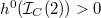 .
.DOI Code:
10.1285/i15900932v36n2p77
Keywords:
General quintic $3$-fold; rational curve; Clemens' conjecture
Full Text: PDF


