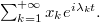Ingham type inequalities towards Parseval equality
Abstract
We consider Trigonometric series with real exponents 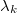 :
: 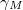 between
between 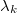 , we show the inequality \begin{equation*}\label{conf000} \frac {2\pi}{\gamma_M(2-c_M)}\sum_{n=1}^M\vert x_n\vert^2 \leq \int_{-\pi/\gamma_M}^{\pi/\gamma_M}\vert \sum_{k=1}^{M} x_ke^{i \lambda_kt}\vert^2dt\leq \frac {2\pi}{c_M\gamma_M} \sum_{n=1}^M\vert x_n\vert^2 \end{equation*} and we show for a class of problems that the limit as
, we show the inequality \begin{equation*}\label{conf000} \frac {2\pi}{\gamma_M(2-c_M)}\sum_{n=1}^M\vert x_n\vert^2 \leq \int_{-\pi/\gamma_M}^{\pi/\gamma_M}\vert \sum_{k=1}^{M} x_ke^{i \lambda_kt}\vert^2dt\leq \frac {2\pi}{c_M\gamma_M} \sum_{n=1}^M\vert x_n\vert^2 \end{equation*} and we show for a class of problems that the limit as 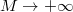 leads to the Parseval's equality. The role of constants
leads to the Parseval's equality. The role of constants 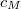 in the above formula is one of the key points of the paper
in the above formula is one of the key points of the paper
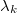 :
: Under an assumption on the gap
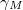 between
between 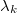 , we show the inequality \begin{equation*}\label{conf000} \frac {2\pi}{\gamma_M(2-c_M)}\sum_{n=1}^M\vert x_n\vert^2 \leq \int_{-\pi/\gamma_M}^{\pi/\gamma_M}\vert \sum_{k=1}^{M} x_ke^{i \lambda_kt}\vert^2dt\leq \frac {2\pi}{c_M\gamma_M} \sum_{n=1}^M\vert x_n\vert^2 \end{equation*} and we show for a class of problems that the limit as
, we show the inequality \begin{equation*}\label{conf000} \frac {2\pi}{\gamma_M(2-c_M)}\sum_{n=1}^M\vert x_n\vert^2 \leq \int_{-\pi/\gamma_M}^{\pi/\gamma_M}\vert \sum_{k=1}^{M} x_ke^{i \lambda_kt}\vert^2dt\leq \frac {2\pi}{c_M\gamma_M} \sum_{n=1}^M\vert x_n\vert^2 \end{equation*} and we show for a class of problems that the limit as 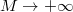 leads to the Parseval's equality. The role of constants
leads to the Parseval's equality. The role of constants 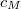 in the above formula is one of the key points of the paper
in the above formula is one of the key points of the paperKeywords:
Trigonometric polynomials; inequalities; Parseval equality
Full Text: PDF