Une conjecture sur les suites centrales d’une boucle de Moufang commutative libre
Abstract
The lower and upper central series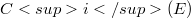 
and 
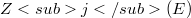of a CML (commutative Moufang loop) E are defined just as the central series of a group, the associators 
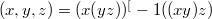playing the same role as the commutators for groups.As was skown recently, if 
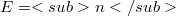(resp.
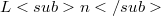) is the free CML (resp. exponent 3 CML) on 
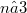generators, the common length of the central series is exactly 
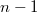. Besides 
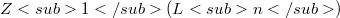contains a torsion-free abelian group 
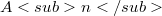of rank n such that 
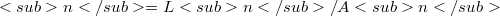.In view of WITT's result about the central series of "the free nilpotent groups of bounded class" we conjecture that the inclusion: 
is in fact an equality in .In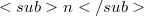 
, this would imply that 
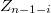is the direct product of 
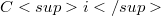by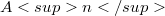 
.The required equalities will be actually checked when either i=1 or $n≤ 4.
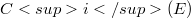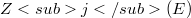and of a CML (commutative Moufang loop) E are defined just as the central series of a group, the associators 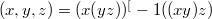playing the same role as the commutators for groups.As was skown recently, if 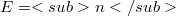(resp.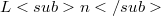) is the free CML (resp. exponent 3 CML) on 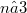generators, the common length of the central series is exactly 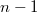. Besides 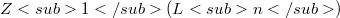contains a torsion-free abelian group 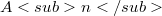of rank n such that 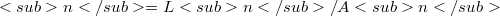.In view of WITT's result about the central series of "the free nilpotent groups of bounded class" we conjecture that the inclusion: 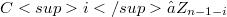is in fact an equality 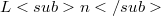in .In 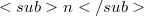, this would imply that 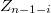is the direct product of 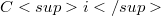by 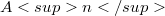.The required equalities will be actually checked when either i=1 or $n≤ 4.DOI Code:
10.1285/i15900932v3n1p45
Full Text: PDF
