Une conjecture sur les suites centrales d’une boucle de Moufang commutative libre
Abstract
The lower and upper central series 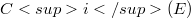 and
and 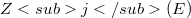 of a CML (commutative Moufang loop) E are defined just as the central series of a group, the associators
of a CML (commutative Moufang loop) E are defined just as the central series of a group, the associators 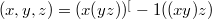 playing the same role as the commutators for groups.As was skown recently, if
playing the same role as the commutators for groups.As was skown recently, if 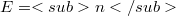 (resp.
(resp.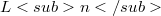 ) is the free CML (resp. exponent 3 CML) on
) is the free CML (resp. exponent 3 CML) on 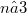 generators, the common length of the central series is exactly
generators, the common length of the central series is exactly 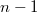 . Besides
. Besides 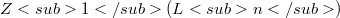 contains a torsion-free abelian group
contains a torsion-free abelian group 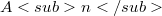 of rank n such that
of rank n such that 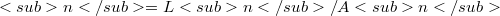 .In view of WITT's result about the central series of "the free nilpotent groups of bounded class" we conjecture that the inclusion:
.In view of WITT's result about the central series of "the free nilpotent groups of bounded class" we conjecture that the inclusion:  is in fact an equality in
is in fact an equality in  .In
.In 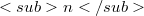 , this would imply that
, this would imply that 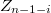 is the direct product of
is the direct product of 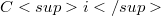 by
by 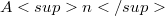 .The required equalities will be actually checked when either i=1 or $n≤ 4.
.The required equalities will be actually checked when either i=1 or $n≤ 4.
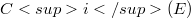 and
and 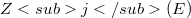 of a CML (commutative Moufang loop) E are defined just as the central series of a group, the associators
of a CML (commutative Moufang loop) E are defined just as the central series of a group, the associators 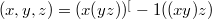 playing the same role as the commutators for groups.As was skown recently, if
playing the same role as the commutators for groups.As was skown recently, if 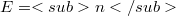 (resp.
(resp.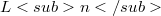 ) is the free CML (resp. exponent 3 CML) on
) is the free CML (resp. exponent 3 CML) on 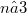 generators, the common length of the central series is exactly
generators, the common length of the central series is exactly 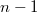 . Besides
. Besides 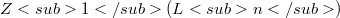 contains a torsion-free abelian group
contains a torsion-free abelian group 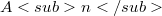 of rank n such that
of rank n such that 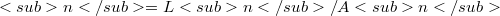 .In view of WITT's result about the central series of "the free nilpotent groups of bounded class" we conjecture that the inclusion:
.In view of WITT's result about the central series of "the free nilpotent groups of bounded class" we conjecture that the inclusion:  is in fact an equality in
is in fact an equality in  .In
.In 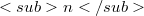 , this would imply that
, this would imply that 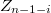 is the direct product of
is the direct product of 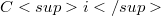 by
by 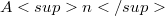 .The required equalities will be actually checked when either i=1 or $n≤ 4.
.The required equalities will be actually checked when either i=1 or $n≤ 4.DOI Code:
10.1285/i15900932v3n1p45
Full Text: PDF


