Some surjectivity results for a class of multivalued maps and applications
Abstract
Let X be a Banach space over k (R or 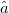 ) and let
) and let 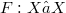 be a multivalued upper semicontinuous (u.s.c.) map with acyclic values. In [MV] Martelli and Vignoli extended to multivalued maps F the definition of a quasinorm of F (notation
be a multivalued upper semicontinuous (u.s.c.) map with acyclic values. In [MV] Martelli and Vignoli extended to multivalued maps F the definition of a quasinorm of F (notation 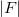 ) given by Granas in [Gr] for singlevalued ones.Using this definition they gave some surjectivity results in the context of 𝛼-nonexpansive and condensing maps with
) given by Granas in [Gr] for singlevalued ones.Using this definition they gave some surjectivity results in the context of 𝛼-nonexpansive and condensing maps with 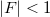 .
In the present paper we improve these results in two ways. Firstly, we use the numerical radius of F (notation
.
In the present paper we improve these results in two ways. Firstly, we use the numerical radius of F (notation 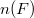 ) instead of the quasinorm of F (we have
) instead of the quasinorm of F (we have 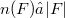 and there exist examples showing that this inequality can be strict). Secondly, we consider the class of admissible maps, which contains the u.s.c. acyclic valued ones.As a consequence we obtain, in particular, surjectivity results for the sum of two singlevalued maps not necessarily one-to-one.We will see that such results could not be obtained by using u.s.c. acyclic valued maps instead of admissible maps.It seems that only Webb [W] has obtained some surjectivity results of this kind.
and there exist examples showing that this inequality can be strict). Secondly, we consider the class of admissible maps, which contains the u.s.c. acyclic valued ones.As a consequence we obtain, in particular, surjectivity results for the sum of two singlevalued maps not necessarily one-to-one.We will see that such results could not be obtained by using u.s.c. acyclic valued maps instead of admissible maps.It seems that only Webb [W] has obtained some surjectivity results of this kind.
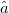 ) and let
) and let 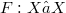 be a multivalued upper semicontinuous (u.s.c.) map with acyclic values. In [MV] Martelli and Vignoli extended to multivalued maps F the definition of a quasinorm of F (notation
be a multivalued upper semicontinuous (u.s.c.) map with acyclic values. In [MV] Martelli and Vignoli extended to multivalued maps F the definition of a quasinorm of F (notation 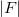 ) given by Granas in [Gr] for singlevalued ones.Using this definition they gave some surjectivity results in the context of 𝛼-nonexpansive and condensing maps with
) given by Granas in [Gr] for singlevalued ones.Using this definition they gave some surjectivity results in the context of 𝛼-nonexpansive and condensing maps with 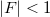 .
In the present paper we improve these results in two ways. Firstly, we use the numerical radius of F (notation
.
In the present paper we improve these results in two ways. Firstly, we use the numerical radius of F (notation 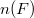 ) instead of the quasinorm of F (we have
) instead of the quasinorm of F (we have 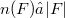 and there exist examples showing that this inequality can be strict). Secondly, we consider the class of admissible maps, which contains the u.s.c. acyclic valued ones.As a consequence we obtain, in particular, surjectivity results for the sum of two singlevalued maps not necessarily one-to-one.We will see that such results could not be obtained by using u.s.c. acyclic valued maps instead of admissible maps.It seems that only Webb [W] has obtained some surjectivity results of this kind.
and there exist examples showing that this inequality can be strict). Secondly, we consider the class of admissible maps, which contains the u.s.c. acyclic valued ones.As a consequence we obtain, in particular, surjectivity results for the sum of two singlevalued maps not necessarily one-to-one.We will see that such results could not be obtained by using u.s.c. acyclic valued maps instead of admissible maps.It seems that only Webb [W] has obtained some surjectivity results of this kind.DOI Code:
10.1285/i15900932v7n2p231
Full Text: PDF


