Convex hypersurfaces with transnormal horizons are spheres
Abstract
Let M be a smooth 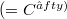 , compact, connected hypersurface of Euclidean
, compact, connected hypersurface of Euclidean 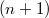 -space
-space 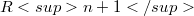 ,
,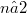 , with nowhere-zero Gaussian curvature. Thus M is differeomorphic to the n-sphere
, with nowhere-zero Gaussian curvature. Thus M is differeomorphic to the n-sphere 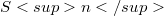 and every affine tangent hyperplane meets M in just one point.Let λ be any (straight) line in
and every affine tangent hyperplane meets M in just one point.Let λ be any (straight) line in 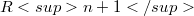 and let
and let 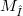 denote the set of points of M at which the tangent hyperplane is parallel to λ.We call
denote the set of points of M at which the tangent hyperplane is parallel to λ.We call 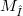 the λ-horizon of M. If, for every λ,
the λ-horizon of M. If, for every λ, 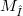 is a transnormal submanifold of
is a transnormal submanifold of 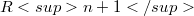 [5] we shall say that M is horizon-transnormal.In this paper we show that if M is horizon-transnormal then M is a round sphere.The converse is obviously true.We show in §2 that if M is horizon-transnormal then it is transnormal.If M is transnormal then every λ-outline ω_(Error rendering LaTeX formula)M_λ$ is contained in a hyperplane normal to λ.It is then a consequence of a classical result that M must be an n-ellipsoid. Consequently, due to its transnormality, M is a round n-sphere.
[5] we shall say that M is horizon-transnormal.In this paper we show that if M is horizon-transnormal then M is a round sphere.The converse is obviously true.We show in §2 that if M is horizon-transnormal then it is transnormal.If M is transnormal then every λ-outline ω_(Error rendering LaTeX formula)M_λ$ is contained in a hyperplane normal to λ.It is then a consequence of a classical result that M must be an n-ellipsoid. Consequently, due to its transnormality, M is a round n-sphere.
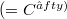 , compact, connected hypersurface of Euclidean
, compact, connected hypersurface of Euclidean 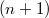 -space
-space 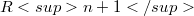 ,
,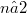 , with nowhere-zero Gaussian curvature. Thus M is differeomorphic to the n-sphere
, with nowhere-zero Gaussian curvature. Thus M is differeomorphic to the n-sphere 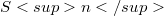 and every affine tangent hyperplane meets M in just one point.Let λ be any (straight) line in
and every affine tangent hyperplane meets M in just one point.Let λ be any (straight) line in 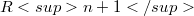 and let
and let 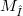 denote the set of points of M at which the tangent hyperplane is parallel to λ.We call
denote the set of points of M at which the tangent hyperplane is parallel to λ.We call 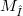 the λ-horizon of M. If, for every λ,
the λ-horizon of M. If, for every λ, 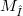 is a transnormal submanifold of
is a transnormal submanifold of 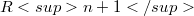 [5] we shall say that M is horizon-transnormal.In this paper we show that if M is horizon-transnormal then M is a round sphere.The converse is obviously true.We show in §2 that if M is horizon-transnormal then it is transnormal.If M is transnormal then every λ-outline ω_(Error rendering LaTeX formula)M_λ$ is contained in a hyperplane normal to λ.It is then a consequence of a classical result that M must be an n-ellipsoid. Consequently, due to its transnormality, M is a round n-sphere.
[5] we shall say that M is horizon-transnormal.In this paper we show that if M is horizon-transnormal then M is a round sphere.The converse is obviously true.We show in §2 that if M is horizon-transnormal then it is transnormal.If M is transnormal then every λ-outline ω_(Error rendering LaTeX formula)M_λ$ is contained in a hyperplane normal to λ.It is then a consequence of a classical result that M must be an n-ellipsoid. Consequently, due to its transnormality, M is a round n-sphere.DOI Code:
10.1285/i15900932v7n2p167
Full Text: PDF


