The annihilator ideal graph of a commutative ring
Abstract
Let 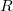 be a commutative ring with nonzero identity and
be a commutative ring with nonzero identity and 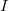 be a proper ideal of
be a proper ideal of 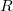 . The annihilator graph of
. The annihilator graph of 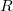 with respect to
with respect to 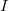 , which is denoted by
, which is denoted by 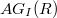 , is the undirected graph with vertex-set
, is the undirected graph with vertex-set 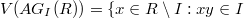 for some
for some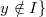 and two distinct vertices
and two distinct vertices  and
and 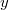 are adjacent if and only if
are adjacent if and only if 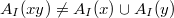 , where
, where 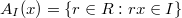 . In this paper, we study some basic properties of
. In this paper, we study some basic properties of 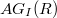 , and we characterise when
, and we characterise when 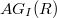 is planar, outerplanar or a ring graph. Also, we study the graph
is planar, outerplanar or a ring graph. Also, we study the graph 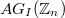 , where
, where 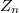 is the ring of integers modulo
is the ring of integers modulo 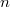 .
.
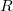 be a commutative ring with nonzero identity and
be a commutative ring with nonzero identity and 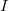 be a proper ideal of
be a proper ideal of 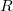 . The annihilator graph of
. The annihilator graph of 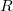 with respect to
with respect to 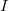 , which is denoted by
, which is denoted by 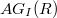 , is the undirected graph with vertex-set
, is the undirected graph with vertex-set 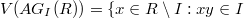 for some
for some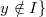 and two distinct vertices
and two distinct vertices  and
and 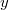 are adjacent if and only if
are adjacent if and only if 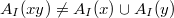 , where
, where 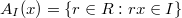 . In this paper, we study some basic properties of
. In this paper, we study some basic properties of 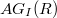 , and we characterise when
, and we characterise when 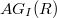 is planar, outerplanar or a ring graph. Also, we study the graph
is planar, outerplanar or a ring graph. Also, we study the graph 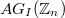 , where
, where 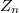 is the ring of integers modulo
is the ring of integers modulo 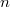 .
.DOI Code:
10.1285/i15900932v36n1p1
Keywords:
Zero-divisor graph; Annihilator graph; Girth; Planar graph; Outerplanar; Ring graph
Full Text: PDF


