Conformally flat immersions
Abstract
A conformally flat manifold (C.F. manifold for short) is a differentiable manifold together with an atlas whose change of coordinate are conformal diffeomorphisms. In terms of Riemannian geometry a C.F. manifold is a Ricmannian manifold such that each point has an open neighborhood conformally diffeomorphic to an open set of an euclidean space. We will take always this point of view. Since space forms (i.e. spaces of constant curvature) of the same dimension are all locally conformally diffeomorphic, C.F. manifolds may be considered as the analogue of such spaces in the context of conformal geometry. Examples of C.F. manifolds are, besides space forms, all two dimensional Riemannian manifolds (due to the existence of isoterma1 coordinates) and products of two space forms of curvature 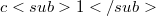 and
and 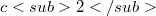 with
with 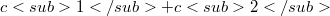 . We observe explicitly that the product of two space forms is not in general a C.F. manifold (see remarks below 2.3) SO the category of C.F. manifolds is not closed under products. In this paper we will study some of the local and global geometry of C.F. manifolds which can be isometrically immersed in euclidean space with low codimension.
. We observe explicitly that the product of two space forms is not in general a C.F. manifold (see remarks below 2.3) SO the category of C.F. manifolds is not closed under products. In this paper we will study some of the local and global geometry of C.F. manifolds which can be isometrically immersed in euclidean space with low codimension.
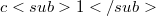 and
and 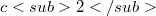 with
with 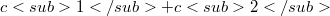 . We observe explicitly that the product of two space forms is not in general a C.F. manifold (see remarks below 2.3) SO the category of C.F. manifolds is not closed under products. In this paper we will study some of the local and global geometry of C.F. manifolds which can be isometrically immersed in euclidean space with low codimension.
. We observe explicitly that the product of two space forms is not in general a C.F. manifold (see remarks below 2.3) SO the category of C.F. manifolds is not closed under products. In this paper we will study some of the local and global geometry of C.F. manifolds which can be isometrically immersed in euclidean space with low codimension.DOI Code:
10.1285/i15900932v9supp85
Full Text: PDF


