(DF)-Spaces of type 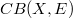 and
and 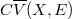
Abstract
Some locally convex properties of the spaces 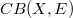 of the bounded continuous functions on a completely regular Hausdorff space X with values in a (DF-space) E are studied and applied to the (DF)-spaces of type
of the bounded continuous functions on a completely regular Hausdorff space X with values in a (DF-space) E are studied and applied to the (DF)-spaces of type 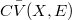 (e.g., see [S]).The following are our main results:
1.
(e.g., see [S]).The following are our main results:
1.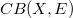 is a (DF)-space if and only if E is a (DF)-space.
2.For a (DF)-space E,
is a (DF)-space if and only if E is a (DF)-space.
2.For a (DF)-space E, 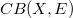 is quasi barrelled if and only if either (i)X is pseudocompact and E is quasibarrelled or (ii) X is not pseudocompact and the bounded subsets of E are metrizaable.
3. If
is quasi barrelled if and only if either (i)X is pseudocompact and E is quasibarrelled or (ii) X is not pseudocompact and the bounded subsets of E are metrizaable.
3. If 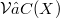 and if each
and if each 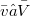 is dominated by some
is dominated by some 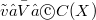 , then
, then 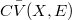 (resp.,
(resp., 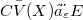 ) is a (DF)-space if and only if E is a (DF)-space.
4. Let X be a locally compact and σ-compact space,
) is a (DF)-space if and only if E is a (DF)-space.
4. Let X be a locally compact and σ-compact space, 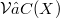 and E a (DF)-space. Then
and E a (DF)-space. Then 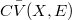 is quasibarrelled if and only if (i) E is quasibarrelled and
is quasibarrelled if and only if (i) E is quasibarrelled and 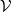 satisfies condition
satisfies condition 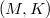 or (ii) the bounded subsets of E are metrizable and
or (ii) the bounded subsets of E are metrizable and 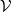 satisfies condition (D).
satisfies condition (D).
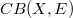 of the bounded continuous functions on a completely regular Hausdorff space X with values in a (DF-space) E are studied and applied to the (DF)-spaces of type
of the bounded continuous functions on a completely regular Hausdorff space X with values in a (DF-space) E are studied and applied to the (DF)-spaces of type 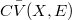 (e.g., see [S]).The following are our main results:
1.
(e.g., see [S]).The following are our main results:
1.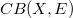 is a (DF)-space if and only if E is a (DF)-space.
2.For a (DF)-space E,
is a (DF)-space if and only if E is a (DF)-space.
2.For a (DF)-space E, 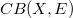 is quasi barrelled if and only if either (i)X is pseudocompact and E is quasibarrelled or (ii) X is not pseudocompact and the bounded subsets of E are metrizaable.
3. If
is quasi barrelled if and only if either (i)X is pseudocompact and E is quasibarrelled or (ii) X is not pseudocompact and the bounded subsets of E are metrizaable.
3. If 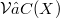 and if each
and if each 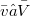 is dominated by some
is dominated by some 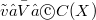 , then
, then 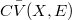 (resp.,
(resp., 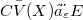 ) is a (DF)-space if and only if E is a (DF)-space.
4. Let X be a locally compact and σ-compact space,
) is a (DF)-space if and only if E is a (DF)-space.
4. Let X be a locally compact and σ-compact space, 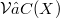 and E a (DF)-space. Then
and E a (DF)-space. Then 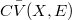 is quasibarrelled if and only if (i) E is quasibarrelled and
is quasibarrelled if and only if (i) E is quasibarrelled and 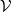 satisfies condition
satisfies condition 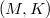 or (ii) the bounded subsets of E are metrizable and
or (ii) the bounded subsets of E are metrizable and 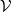 satisfies condition (D).
satisfies condition (D).DOI Code:
10.1285/i15900932v10supn1p127
Full Text: PDF


