On collinearity, parallelism and sphericity for pairs of curves
Abstract
The relationship between the notions of collinearity and equichordality [1] is similar to the one between the notions of parallelism and self-parallelism [2]. In [1] some results concerning self-parallelism, equichordality and sphericity were proved.It is therefore natural to look for analogous results but now relating the ideas of parallelism, collinearity and sphericity.This is what we aim at in section 3 of this short note.For simplicity we shall consider only embeddings of 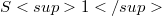 into
into 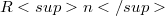 but the proofs work equally well if we replace
but the proofs work equally well if we replace 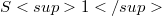 by a compact, connected, smooth manifold.In section 4 we deal with collinear equichordal embeddings and make a few simple considerations on lengths and chordal areas.
by a compact, connected, smooth manifold.In section 4 we deal with collinear equichordal embeddings and make a few simple considerations on lengths and chordal areas.
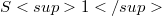 into
into 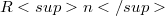 but the proofs work equally well if we replace
but the proofs work equally well if we replace 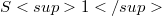 by a compact, connected, smooth manifold.In section 4 we deal with collinear equichordal embeddings and make a few simple considerations on lengths and chordal areas.
by a compact, connected, smooth manifold.In section 4 we deal with collinear equichordal embeddings and make a few simple considerations on lengths and chordal areas.DOI Code:
10.1285/i15900932v10n1p135
Full Text: PDF


