Remarks on compactness of operators defined on 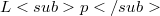
Abstract
This note presents several observations on Banach spaces X such that, for fixed 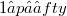 , every operator from an
, every operator from an 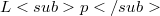 -space into X which is weakly compact is already compact.The interest in such objects is due to the fact that a Banach space X has the above property for
-space into X which is weakly compact is already compact.The interest in such objects is due to the fact that a Banach space X has the above property for 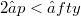 if and only if, for some and then all
if and only if, for some and then all 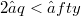 , every strictly q-integral operator with values in X is already q-integral. Recall that a Banach space X has the Radon-Nikodym property iff every strictly 1 -integral X-valued operator is nuclear. We shall, however, not discuss any Radon-Nikodym aspects here;these can be found in C. Cardassi's theory [3].
, every strictly q-integral operator with values in X is already q-integral. Recall that a Banach space X has the Radon-Nikodym property iff every strictly 1 -integral X-valued operator is nuclear. We shall, however, not discuss any Radon-Nikodym aspects here;these can be found in C. Cardassi's theory [3].
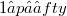 , every operator from an
, every operator from an 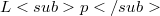 -space into X which is weakly compact is already compact.The interest in such objects is due to the fact that a Banach space X has the above property for
-space into X which is weakly compact is already compact.The interest in such objects is due to the fact that a Banach space X has the above property for 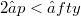 if and only if, for some and then all
if and only if, for some and then all 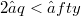 , every strictly q-integral operator with values in X is already q-integral. Recall that a Banach space X has the Radon-Nikodym property iff every strictly 1 -integral X-valued operator is nuclear. We shall, however, not discuss any Radon-Nikodym aspects here;these can be found in C. Cardassi's theory [3].
, every strictly q-integral operator with values in X is already q-integral. Recall that a Banach space X has the Radon-Nikodym property iff every strictly 1 -integral X-valued operator is nuclear. We shall, however, not discuss any Radon-Nikodym aspects here;these can be found in C. Cardassi's theory [3].DOI Code:
10.1285/i15900932v11p225
Full Text: PDF


