Quotients of Raikov-complete topological groups
Abstract
A topological group X is called Raikov-complete if the two sides uniformity on X, that is the supremum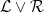 
of the left uniformity and the right uniformity 
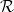on X, is complete.It will be proved that the quotient 
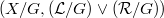of an inframetrizable Raikov-complete topological group X with a neutral subgroup G is complete.(If G is normal (and therefore neutral), the completeness of 
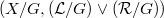is equivalent to the Raikov-completeness of the quotient group 
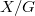).The proof consist in an intricate lifting of 
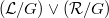-Cauchy filters. Where it is possible, the results on topological groups will be derived from results on uniform spaces.
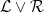of the left uniformity and the right uniformity 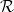on X, is complete.It will be proved that the quotient 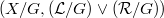of an inframetrizable Raikov-complete topological group X with a neutral subgroup G is complete.(If G is normal (and therefore neutral), the completeness of 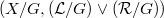is equivalent to the Raikov-completeness of the quotient group 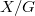).The proof consist in an intricate lifting of 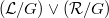-Cauchy filters. Where it is possible, the results on topological groups will be derived from results on uniform spaces.DOI Code:
10.1285/i15900932v13n1p75
Classification:
54E15; 54E50; 22A05
Full Text: PDF
