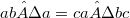Quadratical groupoids
Abstract
A groupoid 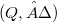 is said to be quadratical if the identity (1)
is said to be quadratical if the identity (1) 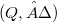 is a right quasigroup, i.e. for any
is a right quasigroup, i.e. for any 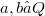 the equation
the equation 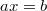 has the unique solution x. Quadratical groupoids arose originally from the geometric situation described in Example 3 below.In this paper we study abstract quadratical groupoids and certain derived algebraic structures.
has the unique solution x. Quadratical groupoids arose originally from the geometric situation described in Example 3 below.In this paper we study abstract quadratical groupoids and certain derived algebraic structures.
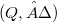 is said to be quadratical if the identity (1)
is said to be quadratical if the identity (1) holds and if
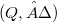 is a right quasigroup, i.e. for any
is a right quasigroup, i.e. for any 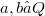 the equation
the equation 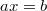 has the unique solution x. Quadratical groupoids arose originally from the geometric situation described in Example 3 below.In this paper we study abstract quadratical groupoids and certain derived algebraic structures.
has the unique solution x. Quadratical groupoids arose originally from the geometric situation described in Example 3 below.In this paper we study abstract quadratical groupoids and certain derived algebraic structures.DOI Code:
10.1285/i15900932v13n1p107
Full Text: PDF