Quasinormable spaces of holomorphic functions
Abstract
Quasinormable spaces were introduced by Grothendieck [34] as a collection of spaces, with good stability properties, which included all Banach spaces and al1 nuclear spaces (a recent article of Meise-Vogt [44] quantifies this statement in an elegant fashion for Fréchet spaces). Quasinormable spaces in which the bounded sets are precompact are called Schwartz spaces and form a more restrictive but even more stable class of spaces (they are closed under the formation of arbitrary products and quotients).In this article we study these properties on space of holomorphic functions with the three standard topologies of infinite dimensional holomorphy,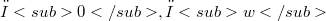 
and 
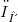. In the presence of one or more of a variety of countability conditions on the underlying locally convex space we found that the spaces of holomorphic functions turned out to be either quasinormable or Schwartz spaces.The compact open topology, 
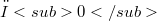and nuclear spaces both enjoy intrinsic compactess properties and in these cases (§1 and 2) we found it possible to study directly the Schwartz property. For the 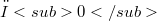topology our countability conditions were-each compact set is contained in the absolutely convex hull of a null sequence, sequential completeness,and each null sequence is Mackey null.We only considered the 
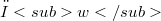and 
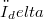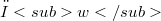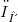topologies on nuclear spaces as the result for the compact open topology is well known and we assumed the existence of a basis and a property which can be compared on the one hand to the defining property of A-nuclear spaces and on the other hand to the sequence space characterization of Schwartz spaces.To obtain general results for the and topologies we used countable neighbourhood systems (in Fréchet spaces) and countable systems of bounded sets (in 
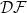spaces) together with S-absolute Schauder decompositions of holomorphic function spaces on balanced domains.
In all cases we found new results which both simplified and contained known results and which suggest further possibilities towards the realization of a more unified theory of locally convex space structures on spaces of holomorphic functions on infinite dimensional domains.
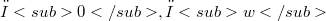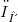and . In the presence of one or more of a variety of countability conditions on the underlying locally convex space we found that the spaces of holomorphic functions turned out to be either quasinormable or Schwartz spaces.The compact open topology, 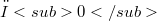and nuclear spaces both enjoy intrinsic compactess properties and in these cases (§1 and 2) we found it possible to study directly the Schwartz property. 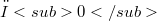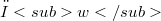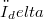For the topology our countability conditions were-each compact set is contained in the absolutely convex hull of a null sequence, sequential completeness,and each null sequence is Mackey null.We only considered the and topologies on nuclear spaces as the result for the compact open topology is well known and we assumed the existence of a basis and a property which can be compared on the one hand to the defining property of A-nuclear spaces and on the other hand to the sequence space characterization of Schwartz spaces.To obtain general results for the 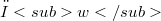and 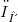topologies we used countable neighbourhood systems (in Fréchet spaces) and countable systems of bounded sets (in spaces) together with S-absolute Schauder decompositions of holomorphic function spaces on balanced domains.
In all cases we found new results which both simplified and contained known results and which suggest further possibilities towards the realization of a more unified theory of locally convex space structures on spaces of holomorphic functions on infinite dimensional domains.DOI Code:
10.1285/i15900932v13n1p155
Classification:
53C10; 53C40
Full Text: PDF
