Isomorphisms between spaces of holomorphic mappings on Banach spaces
Abstract
Let 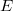 and
and 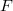 be Banach spaces. Our objective in this work is to find conditions under which, whenever the topological dual spaces
be Banach spaces. Our objective in this work is to find conditions under which, whenever the topological dual spaces 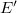 and
and 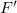 are isomorphic, the spaces of holomorphic mappings of bounded type on
are isomorphic, the spaces of holomorphic mappings of bounded type on 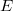 and
and 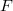 are isomorphic as well. We also examine the corresponding problem for the spaces of holomorphic mappings of a certain type, for instance nuclear bounded type, compact bounded type or weakly compact bounded type.
are isomorphic as well. We also examine the corresponding problem for the spaces of holomorphic mappings of a certain type, for instance nuclear bounded type, compact bounded type or weakly compact bounded type.
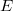 and
and 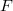 be Banach spaces. Our objective in this work is to find conditions under which, whenever the topological dual spaces
be Banach spaces. Our objective in this work is to find conditions under which, whenever the topological dual spaces 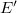 and
and 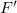 are isomorphic, the spaces of holomorphic mappings of bounded type on
are isomorphic, the spaces of holomorphic mappings of bounded type on 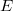 and
and 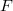 are isomorphic as well. We also examine the corresponding problem for the spaces of holomorphic mappings of a certain type, for instance nuclear bounded type, compact bounded type or weakly compact bounded type.
are isomorphic as well. We also examine the corresponding problem for the spaces of holomorphic mappings of a certain type, for instance nuclear bounded type, compact bounded type or weakly compact bounded type.DOI Code:
10.1285/i15900932v31n2p1
Keywords:
Banach space ; Holomorphic mappings ; Isomorphisms
Full Text: PDF


