Heegaard splittings of the Brieskorn homology spheres that are equivalent after one stabilization

doi:10.1285/i15900932v20n1p53

Heegaard splittings of the Brieskorn homology spheres that are equivalent after one stabilization

Young Ho Im, Hwan Kim Kim

Abstract

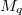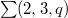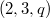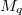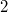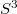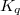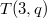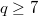We construct a class of 3-manifolds $M_q$ which are homeomorphic to the Brieskorn homology spheres $\sum(2,3,q)$ , where $(2,3,q)$ are relatively prime. Also, we show that $M_q$ is a $2$ -fold cyclic branched covering of $S^3$ over a knot $K_q$ which is inequivalent with torus knot $T(3,q)$ for $q \ge 7$ . 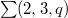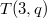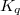Moreover, we show that two inequivalent Heegaard splittings of $\sum(2,3,q)$ of genus 2 associated with $T(3,q)$ and $K_q$ are equivalent after single stabilization.