A criterion for a group to be nilpotent
Abstract
Let 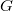 be a group with
be a group with 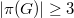 . In this paper it is shown that
. In this paper it is shown that 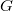 is nilpotent if and only if for every subgroup
is nilpotent if and only if for every subgroup 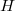 of
of 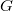 with
with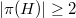 we have
we have 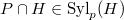 for each
for each 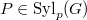 and for every
and for every 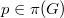 .
.
DOI Code:
10.1285/i15900932v20n1p33
Keywords:
Nilpotent; Sylow subgroups; Intersections of Sylow subgroups with subgroups
Classification:
20D15; 20D20
Full Text: PDF


