Selection principles and the Minimal Tower problem


Abstract


We study diagonalizations of covers using various selectionprinciples, where the covers are related to linearquasiorderings (\tau-covers).This includes: equivalences and nonequivalences,combinatorial characterizations, critical cardinalities andconstructions of special sets of reals.This study leads to a solution of a topological problem which wassuggested to the author by Scheepers (and stated in [15]) and is related to the Minimal Tower problem.

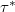We also introduce a variant of the notion of \tau-cover,called \tau^*-cover, and settle some problems for thisvariant which are still open in the case of \tau-covers.This new variant introduces new (and tighter) topologicaland combinatorial lower bounds on the Minimal Tower problem.


DOI Code: 10.1285/i15900932v22n2p53

Keywords: Gerlits-Nagy property $gamma$-sets; $gamma$-cover; $omega$-cover; $ au$-cover; Tower; Selection principles; Borel covers; Open covers

Classification: 03E05; 54D20; 54D80

Full Text: PDF
کاغذ a4

Creative Commons License
This work is licensed under a Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0 Italia License.