The Pytkeev property and the Reznichenko property in function spaces


Abstract


For a Tychonoff space 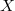X we denote by 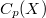C_p(X) the space of all real-valued continuous functions on 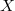X with the topology of pointwise convergence. Characterizations of sequentiality and countable tightness of 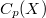C_p(X) in terms of 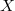X were given by Gerlits, Nagy, Pytkeev and Arhangel'skii.  In this paper, we characterize the Pytkeev property and the Reznichenko property of 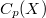C_p(X) in terms of 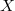X.  In particular we note that if 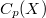C_p(X) over a subset 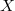X of the real line is a Pytkeev space, then 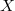X is perfectly meager and has universal measure zero.


DOI Code: 10.1285/i15900932v22n2p43

Keywords: Function space; Topology of pointwise convergence; Sequential; Countable tightness; Pytkeev space; Weakly Fréchet-Urysohn; $omega$ -cover; $omega$-shrinkable; $omega$-grouping property; The Menger property; The Rothberger property; The Hurewicz property; Universal measure zero; Perfectly meager; Property $(gamma)$

Classification: 54C35; 54D20; 54D55; 54H05

Full Text: PDF
کاغذ a4

Creative Commons License
This work is licensed under a Creative Commons Attribuzione - Non commerciale - Non opere derivate 3.0 Italia License.