Aruler and segment-transporter constructive axiomatization of plane hyperbolic geometry
Abstract
We formulate a universal axiom system for plane hyperbolic geometry in a first-order language with one sort of individual variables, points (lower-case), containing three individual constants, 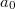 ,
, 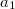 ,
, 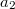 , standing for three non-collinear points, with
, standing for three non-collinear points, with 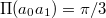 , one quaternary operation symbol
, one quaternary operation symbol 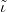 , with
, with 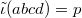 to be interpreted as `
to be interpreted as ` is the point of intersection of lines
is the point of intersection of lines 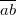 and
and 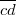 , provided that lines
, provided that lines 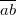 and
and 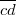 are distinct and have a point of intersection, an arbitrary point, otherwise', and two ternary operation symbols,
are distinct and have a point of intersection, an arbitrary point, otherwise', and two ternary operation symbols, 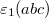 and
and 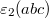 , with
, with 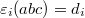 (for
(for 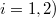 to be interpreted as `
to be interpreted as `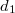 and
and 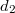 are two distinct points on line
are two distinct points on line 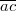 such that
such that 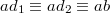 , provided that
, provided that 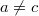 , an arbitrary point, otherwise'.
, an arbitrary point, otherwise'.
DOI Code:
10.1285/i15900932v22n1p1
Keywords:
Hyperbolic geometry; Constructive axiomatization; Quantifier-free axiomatization
Full Text: PDF


