(LB)-spaces and quasi-reflexivity
Abstract
Let 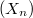 be a sequence of infinite-dimensional Banach spaces. For
be a sequence of infinite-dimensional Banach spaces. For 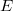 being the space
being the space 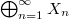 , the following equivalences are shown: 1. Every closed subspace
, the following equivalences are shown: 1. Every closed subspace 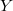 of
of 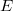 , with the Mackey topology
, with the Mackey topology 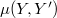 , is an (LB)-space. 2. Every separated quotient of
, is an (LB)-space. 2. Every separated quotient of ![E'\ [\mu(E',E)]](http://siba-ese.unile.it/plugins/generic/latexRender/cache/6f075f7e4260c5ac69ffcd6c19ed53f6.png) \ is locally complete. 3.
\ is locally complete. 3. 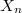 is quasi-reflexive,\
is quasi-reflexive,\ 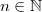 . Besides this, the following two properties are seen to be equivalent: 1.
. Besides this, the following two properties are seen to be equivalent: 1. ![E'\ [\mu(E',E)]](http://siba-ese.unile.it/plugins/generic/latexRender/cache/6f075f7e4260c5ac69ffcd6c19ed53f6.png) has the Krein-
has the Krein-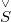 mulian property. 2.
mulian property. 2. 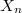 is reflexive,
is reflexive, 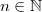 .
.
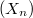 be a sequence of infinite-dimensional Banach spaces. For
be a sequence of infinite-dimensional Banach spaces. For 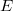 being the space
being the space 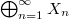 , the following equivalences are shown: 1. Every closed subspace
, the following equivalences are shown: 1. Every closed subspace 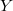 of
of 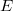 , with the Mackey topology
, with the Mackey topology 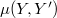 , is an (LB)-space. 2. Every separated quotient of
, is an (LB)-space. 2. Every separated quotient of ![E'\ [\mu(E',E)]](http://siba-ese.unile.it/plugins/generic/latexRender/cache/6f075f7e4260c5ac69ffcd6c19ed53f6.png) \ is locally complete. 3.
\ is locally complete. 3. 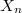 is quasi-reflexive,\
is quasi-reflexive,\ 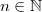 . Besides this, the following two properties are seen to be equivalent: 1.
. Besides this, the following two properties are seen to be equivalent: 1. ![E'\ [\mu(E',E)]](http://siba-ese.unile.it/plugins/generic/latexRender/cache/6f075f7e4260c5ac69ffcd6c19ed53f6.png) has the Krein-
has the Krein-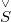 mulian property. 2.
mulian property. 2. 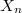 is reflexive,
is reflexive, 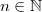 .
.DOI Code:
10.1285/i15900932v31n1p191
Full Text: PDF


