On the domain of a Fleming--Viot-type operator on an 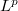 -space with invariant measure
-space with invariant measure
Abstract
We characterize the domain of a Fleming-Viot type operator of the form 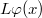 :=
:=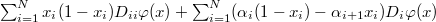 on
on ![L^p([0,1]^N,\mu)](http://siba-ese.unile.it/plugins/generic/latexRender/cache/2164c583e08758181ad616484bc4622f.png) for
for 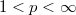 , where
, where 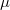 is the corresponding invariant measure. Our approach relies on the characterization of the domain of the one-dimensional Fleming-Viot operator and the Dore-Venni operator sum method.
is the corresponding invariant measure. Our approach relies on the characterization of the domain of the one-dimensional Fleming-Viot operator and the Dore-Venni operator sum method.
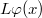 :=
:=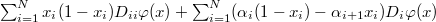 on
on ![L^p([0,1]^N,\mu)](http://siba-ese.unile.it/plugins/generic/latexRender/cache/2164c583e08758181ad616484bc4622f.png) for
for 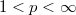 , where
, where 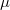 is the corresponding invariant measure. Our approach relies on the characterization of the domain of the one-dimensional Fleming-Viot operator and the Dore-Venni operator sum method.
is the corresponding invariant measure. Our approach relies on the characterization of the domain of the one-dimensional Fleming-Viot operator and the Dore-Venni operator sum method.DOI Code:
10.1285/i15900932v31n1p139
Keywords:
Fleming--Viot process; degenerate elliptic problems; analytic $C_0$-semigroups
Full Text: PDF


