Bohr’s radii and strips – a microscopic and a macroscopic view
Abstract
The Bohr-Bohnenblust-Hille theorem states that the largest possible width 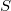 of the strip in the complex plane on which a Dirichlet series
of the strip in the complex plane on which a Dirichlet series 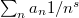 converges uniformly but not absolutely, equals
converges uniformly but not absolutely, equals 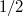 . In fact Bohr in 1913 proved that
. In fact Bohr in 1913 proved that 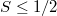 , and asked for equality. The general theory of Dirichlet series during this time was one of the most fashionable topics in analysis, and Bohr's so-called \textit{absolute convergence problem} was very much in the focus. In this context Bohr himself discovered several deep connections of Dirichlet series and power series (holomorphic functions) in infinitely many variables, and as a sort of by-product he found his famous power series theorem. Finally, Bohnenblust and Hille in 1931 in a rather ingenious fashion answered the absolute convergence problem in the positive. In recent years many authors revisited the work of Bohr, Bohnenblust and Hille -- improving this work but also extending it to more general settings, for example to Dirichlet series with coefficients in Banach spaces. The aim of this article is to report on parts of this new development.
, and asked for equality. The general theory of Dirichlet series during this time was one of the most fashionable topics in analysis, and Bohr's so-called \textit{absolute convergence problem} was very much in the focus. In this context Bohr himself discovered several deep connections of Dirichlet series and power series (holomorphic functions) in infinitely many variables, and as a sort of by-product he found his famous power series theorem. Finally, Bohnenblust and Hille in 1931 in a rather ingenious fashion answered the absolute convergence problem in the positive. In recent years many authors revisited the work of Bohr, Bohnenblust and Hille -- improving this work but also extending it to more general settings, for example to Dirichlet series with coefficients in Banach spaces. The aim of this article is to report on parts of this new development.
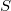 of the strip in the complex plane on which a Dirichlet series
of the strip in the complex plane on which a Dirichlet series 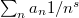 converges uniformly but not absolutely, equals
converges uniformly but not absolutely, equals 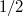 . In fact Bohr in 1913 proved that
. In fact Bohr in 1913 proved that 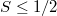 , and asked for equality. The general theory of Dirichlet series during this time was one of the most fashionable topics in analysis, and Bohr's so-called \textit{absolute convergence problem} was very much in the focus. In this context Bohr himself discovered several deep connections of Dirichlet series and power series (holomorphic functions) in infinitely many variables, and as a sort of by-product he found his famous power series theorem. Finally, Bohnenblust and Hille in 1931 in a rather ingenious fashion answered the absolute convergence problem in the positive. In recent years many authors revisited the work of Bohr, Bohnenblust and Hille -- improving this work but also extending it to more general settings, for example to Dirichlet series with coefficients in Banach spaces. The aim of this article is to report on parts of this new development.
, and asked for equality. The general theory of Dirichlet series during this time was one of the most fashionable topics in analysis, and Bohr's so-called \textit{absolute convergence problem} was very much in the focus. In this context Bohr himself discovered several deep connections of Dirichlet series and power series (holomorphic functions) in infinitely many variables, and as a sort of by-product he found his famous power series theorem. Finally, Bohnenblust and Hille in 1931 in a rather ingenious fashion answered the absolute convergence problem in the positive. In recent years many authors revisited the work of Bohr, Bohnenblust and Hille -- improving this work but also extending it to more general settings, for example to Dirichlet series with coefficients in Banach spaces. The aim of this article is to report on parts of this new development.DOI Code:
10.1285/i15900932v31n1p87
Keywords:
Dirichlet series ; Bohr’s strips ; Bohr radii ; inf. dim. holomorphy ; Bohnenblust-Hille inequalities ; Banach spaces
Full Text: PDF


