On a class of positive 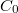 -semigroups of operators on weighted continuous function spaces
-semigroups of operators on weighted continuous function spaces
Abstract
This paper is mainly concerned with the study of the generators of those positive 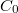 -semigroups on weighted continuous function spaces that leave invariant a given closed sublattice of bounded continuous functions and whose relevant restrictions are Feller semigroups. Additive and multiplicative perturbation results for this class of generators are also established. Finally, some applications concerning multiplicative perturbations of the Laplacian on
-semigroups on weighted continuous function spaces that leave invariant a given closed sublattice of bounded continuous functions and whose relevant restrictions are Feller semigroups. Additive and multiplicative perturbation results for this class of generators are also established. Finally, some applications concerning multiplicative perturbations of the Laplacian on 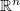 ,
, 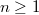 , and degenerate second-order differential operators on unbounded real intervals are showed.
, and degenerate second-order differential operators on unbounded real intervals are showed.
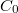 -semigroups on weighted continuous function spaces that leave invariant a given closed sublattice of bounded continuous functions and whose relevant restrictions are Feller semigroups. Additive and multiplicative perturbation results for this class of generators are also established. Finally, some applications concerning multiplicative perturbations of the Laplacian on
-semigroups on weighted continuous function spaces that leave invariant a given closed sublattice of bounded continuous functions and whose relevant restrictions are Feller semigroups. Additive and multiplicative perturbation results for this class of generators are also established. Finally, some applications concerning multiplicative perturbations of the Laplacian on 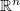 ,
, 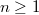 , and degenerate second-order differential operators on unbounded real intervals are showed.
, and degenerate second-order differential operators on unbounded real intervals are showed.DOI Code:
10.1285/i15900932v31n1p15
Keywords:
Positive semigroup ; Feller property ; weighted continuous function space ; evolution equation
Full Text: PDF


