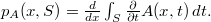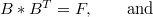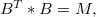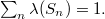Characterization of idempotent 2-copulas

Abstract

A 2-copula 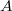induces a transition probability function 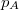via

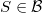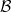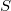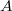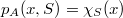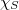where , denoting the Lebesgue measurable subsets of.  We say that a set is invariant under if for almost all , being the characteristic function of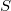.  The sets 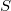invariant under 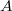form a sub-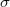-algebra of theLebesgue measurable sets, which we denote 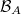. A set 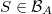is called an atom if it has positive measure and if for any 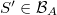, 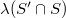is either 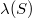or 0.
A 2-copula 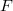is idempotent if 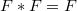. Here denotes the product defined in [1]. Idempotent 2-copulas are classified and characterized asfollows:
(i) An idempotent 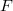is said to be nonatomic if 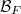contains noatoms.  If 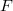is a nonatomic idempotent, then it is the product of a leftinvertible copula and its transpose.  That is, there exists a copula 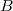such that

where
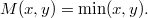
(ii) An idempotent 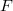is said to be totally atomic if there exist essentiallydisjoint atoms 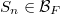with

If 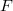is a totally atomic idempotent, then it is conjugate to an ordinal sumof copies of the product copula.  That is, there exists a copula 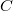satisfying 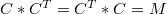and a partition 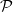of such that
\begin{equation}F=C*(\oplus _{\cal P}F_k)*C^T \end{equation} where eachcomponent 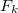in the ordinal sum is the product copula .
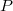(iii) An idempotent 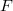is said to be atomic (but not totally atomic) if 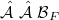contains atoms but the sum of the measures of a maximal collection ofessentially disjoint atoms is strictly less than 1.  In this mixed case, thereexists a copula 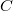invertible with respect to 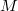and a partition 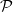of for which (1) holds, with 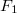being a nonatomic idempotent copula andwith 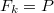for .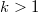
Some of the immediate consequences of this characterization are discussed.