Primes modulo which almost all Fermat numbers are primitive roots
Abstract
A prime  is called elite, or anti-elite, when all but finitely many Fermat numbers are quadratic nonresidues or residues, respectively, modulo
is called elite, or anti-elite, when all but finitely many Fermat numbers are quadratic nonresidues or residues, respectively, modulo  . It is known that if the multiplicative order of 2 modulo
. It is known that if the multiplicative order of 2 modulo  is of the form
is of the form 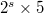 , where
, where 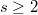 , then the prime
, then the prime  is either elite or anti-elite. Modulo elite primes of this kind, we describe some criteria by which all sufficiently large Fermat numbers be primitive roots, or all nonprimitive roots.
is either elite or anti-elite. Modulo elite primes of this kind, we describe some criteria by which all sufficiently large Fermat numbers be primitive roots, or all nonprimitive roots.
 is called elite, or anti-elite, when all but finitely many Fermat numbers are quadratic nonresidues or residues, respectively, modulo
is called elite, or anti-elite, when all but finitely many Fermat numbers are quadratic nonresidues or residues, respectively, modulo  . It is known that if the multiplicative order of 2 modulo
. It is known that if the multiplicative order of 2 modulo  is of the form
is of the form 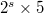 , where
, where 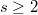 , then the prime
, then the prime  is either elite or anti-elite. Modulo elite primes of this kind, we describe some criteria by which all sufficiently large Fermat numbers be primitive roots, or all nonprimitive roots.
is either elite or anti-elite. Modulo elite primes of this kind, we describe some criteria by which all sufficiently large Fermat numbers be primitive roots, or all nonprimitive roots.DOI Code:
10.1285/i15900932v30n1p133
Keywords:
elite primes; Fermat numbers
elite primes; Fermat numbers
Classification:
11A07, 11A41
Full Text: PDF


